引導自主探索建構探究式數(shù)學教學模式

趙波

【摘 要】本文結合實際教學案例對自主探究教學模式進行論述，教會學生獨立發(fā)現(xiàn)、推導論證，動手操作、探究知識，歸納類比、靈活運用，打破定式、找出聯(lián)系，從而提高學生的自主探究數(shù)學問題的能力，培養(yǎng)學生應用數(shù)學的能力。

【關鍵詞】高中數(shù)學 自主探究 獨立發(fā)現(xiàn) 動手操作 歸納類比 打破定式

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2017）11B-0040-02

自主探究式教學模式是為了更好地引導學生提升能力，改善傳統(tǒng)的傳承式教學模式而提出的一種新興教學模式，這種教學模式與傳統(tǒng)的教學模式除了教學觀念的不同以外，教學方法也不同。自主探究式教學模式是結合信息技術而進行教學的一種模式，它的教學特點既能符合時代的發(fā)展，又對教學進行了創(chuàng)造性的改革，對學生的能力提升有很好的幫助。在教學過程中常用的自主探究教學的方法主要有獨立發(fā)現(xiàn)、動手操作、歸納類比、打破定式等，在教師的引導下利用網(wǎng)絡平臺，讓學生自己進行探究，從而有效地激發(fā)學生的學習興趣，對學生的思想意識建設也更有幫助，也更加適應高中數(shù)學的學科特點，因此深受歡迎。

一、獨立發(fā)現(xiàn)，推導論證

獨立發(fā)現(xiàn)是高中數(shù)學教學中實施自主探究教學模式的一種方法，其主要過程為學生通過獨自猜測、推導等各種方法尋找出教師隱藏在教學情境中的知識。這些知識多是一些重難點知識，讓學生自己探索發(fā)現(xiàn)，從而更加全面地掌握知識。

如在教學“直線、平面平行的判定及位置關系”時，為了能夠讓學生通過教學徹底地掌握二面角的相關知識，筆者在教學時特地采用自主探究的教學模式，以此來引導學生進行自主探究學習。在教學這一節(jié)內容時，筆者采用幾何畫板制作了簡單的教學課件，并將部分知識隱藏在設計的教學情境中。隱藏的知識主要有“二面角的平面角概念”“如何求二面角的平面角”“怎么度量二面角的大小”等知識。在進行教學時，毛筆首先利用已經(jīng)制作完成的簡單課件來引導學生。這個簡單課件包含二面角的概念及其形成過程。當完成教學時，學生從中能夠很快地領悟二面角的概念，并在此基礎上對“隱藏”知識進行探究，從而使學生更加容易地理解和掌握有關二面角的概念及其相關知識。這樣的教學引導能有效地激發(fā)學生的探究欲望，為學生完成探究學習起到導向作用。在探究過程中，學生之間可以就彼此的意見進行交換，以小組為單位進行學習，推導認證。學生在探究中找到教師隱藏在課件背后的知識，從而豐富自己的知識。學生探究得到結果后，教師對學生的探究結果進行修正、補充、點評，最終完成整個自主探究教學。教師在實際教學中運用這種方法時可以進行適當創(chuàng)新，以獲得更好的教學效果。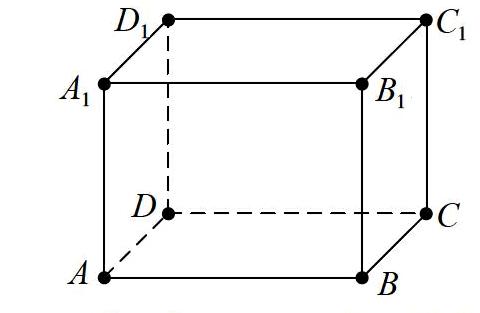

獨立發(fā)現(xiàn)的重點在于學生的探究發(fā)現(xiàn)，但是教師的引導也非常重要，因此，教師在教學中采用這種方法時要設計合適的引導方式，只有這樣才能更好地促進學生進行探究發(fā)現(xiàn)，才能使教學獲得更好的效果。

二、動手操作，探究知識

高中數(shù)學要求學生要有較強的綜合思維能力，其中，動手“思考”問題也是學生必備的一種能力。動手操作使學生自己感知相關知識，理解和掌握一些抽象的知識。

如在教學“空間點、直線、平面之間的位置關系”時，為了更好地引導學生掌握異面直線的相關概念，筆者在教學時采用自主探究教學模式中的動手操作的方法來引導學生進行學習。課本給異面直線的定義是“不同在任何一個平面內的兩條直線叫作異面直線”。這句話比較抽象，因此需要用立方體來幫助理解。為此筆者引導學生利用立方體來探究異面直線的相關直線和性質。在教學相關內容之前，筆者先讓學生用硬紙自己動手制作立方體，并對立方體的各個點進行標注，制作模型如下。

在學生完成了模型制作后，筆者用模型來引導學生理解“異面直線”概念及其相關知識。如讓學生判斷直線 A1B1 與直線 AC 的位置關系，直線 A1B1 與直線 AB 的位置關系，等等，從圖中得出，直線 A1B1 與直線 AB 是典型的同面直線，直線 A1B1 與直線 AC 是異面直線。這樣使學生更加清楚地感知所學的知識，直觀地理解異面直線的概念。學生動手操作制作數(shù)學模型能將抽象的知識直觀化，減小學習難度，提升學習效率，更好地理解抽象的知識，取得良好的學習效果。

三、歸納類比，靈活運用

歸納類比也是自主探究的一種方法，這種方法主要用于對公式、概念、解題等方面的學習。在高中數(shù)學中，歸納類比是學生必備的一種思維方法，用這種方法進行教學非常必要。

如在教學“函數(shù)與方程”時，為了更好地引導學生的解題思路，筆者在教學時特地采用自主探究模式的歸納類比方法，以此來引導學生掌握歸納類比法。在解答數(shù)學題目中運用歸納類比法可以簡化思考過程，有效提升解題效率。如下面的題目：

函數(shù) f（x）定義在 R 上，并且其圖象分別關于直線 x=a 與 x=b 對稱，其中 a>b，試說明該函數(shù)是否為周期函數(shù)？若是周期函數(shù)則求出其周期。

閱讀題目發(fā)現(xiàn)，函數(shù) f（x）有兩個對稱軸，所以將其與函數(shù) y=sinx 相類比。我們知道， 和 是函數(shù) y=sinx 的兩條對稱軸，而且其周期為 ，所以我們可以假設函數(shù) f（x）是周期函數(shù)，設其周期為 2（a-b），這樣，如果能證明假設成立那么就成功地解答出題目。根據(jù)題目中的信息可知，直線 x=a 與 x=b 是該函數(shù)的兩條對稱軸，所以有 f（x）=f（2b-x），有 f（2b-x）=f[2b-（2a-x）]，所以 f（x）=f（x+2b-2a），故該函數(shù)為周期函數(shù)，且周期為 2（a-b）。從這個題目的解答過程可以看出，在解題的時候運用類比推理的方法可以給解題過程帶來很大的方便。

從上面的試題解答過程中可以看出，歸納類比法在高中數(shù)學中具有很大的作用。歸納類比也是高考考查學生的必備能力之一，因此教師在數(shù)學教學中要注意培養(yǎng)學生的歸納類比意識，教會學生歸納類比的思想方法。

四、打破定式，找出聯(lián)系

學習數(shù)學最忌諱的是沒有自己的獨立思想，只會套公式，如果這樣就會出現(xiàn)思想僵化，不能靈活運用所掌握的知識，因此，教師在教學時要引導學生打破定式，突破問題。如在教學“基本不等式”時，為了能夠使學生靈活地運用所學習的知識，筆者特地選擇采用自主探究教學模式的打破定式的方法進行教學，幫助學生靈活掌握知識，靈活運用知識。舉個例題如下：

這道題目是典型的不等式計算的問題，是考試中經(jīng)常會出現(xiàn)的類型題，所以用這一題目測試學生，既能了解學生掌握知識的程度，又能知道學生靈活運用知識的能力。在學生對該試題進行解答時，筆者發(fā)現(xiàn)學生大多數(shù)都是采用基本不等式的方法對該題進行解答，即

對比這兩種解題方法可以看出，第二種方法比第一種方法更為簡便，思考過程更為簡潔。可見采用向量思維解決不等式問題是一種打破定式的一種思維方法。

打破定式不僅僅是針對不等式題目，而且是在整個數(shù)學學習中都需要學生打破定式，只有打破定式才能真正地提升學生的數(shù)學能力，才能使學生學會靈活運用所學習的知識。

綜上所述，自主探究式教學模式比傳統(tǒng)的教學模式更加注重學生能力的發(fā)展，也更加注重學生數(shù)學思維的培養(yǎng)。因此，教師在實際教學中采用這種教學模式時，一定要靈活運用各種方法，以獲得更好的教學效果。

【參考文獻】

[1]嚴雪峰.高中數(shù)學探究式教學模式研究[J].學園，2016（8）

[2]雅 惠.幾何畫板用于高中數(shù)學教學的實踐探究[J].高考，2016（6）

[3]王樹才.高中數(shù)學自主探究模式的應用研究[J].新課程學習，2014（11）

（責編 盧建龍）endprint