緊扣數學本質，深化數學理解

潘靈聰

摘要：數學學習的意義在于理解規則概念、獲得方法策略、體驗思考價值，感受學習愉悅等。教師應該緊扣數學教學的本質，把學習目標變為任務驅動，回歸有意義的數學教學。

關鍵詞：數學本質? 數學理解? 《三角形三邊關系》

小學數學教師需要設立每堂課的教學目標，要基于對教學內容所蘊含的教學價值、思維水平、育人因素進行合理解讀，設計有價值的教學活動。當然，教師也需要合理評估學生的能力，制訂課堂的動態目標。

《三角形三邊關系》是小學數學圖形與幾何領域的重要內容，教材圍繞“通過實驗，發現三角形任意兩邊的和大于第三邊”這一教學目標，附帶了幾組小棒，旨在讓學生用小棒拼成三角形，以便完成數學實驗。然而，學生不明白為什么要這樣做，只是機械地跟隨指示進行實驗，課堂因此而變得乏味無趣。筆者認為，數學課程應該提倡“淡化形式，注重實質”，讓學生經歷數學活動的過程，體驗數學思考方法的重要性。

一、基于學情現狀的重新審視，走近起點，課堂真實自然

數學學習基于經驗，又需超越經驗，學生需要有一種理性探究的精神。要想調動學生有意義的學習，教師應該充分考慮學生的能力和經驗。基于這樣的思考，筆者在課前進行了前測，如表1所示。

在設計前測維度時，教師必須了解學生的原有起點：第一，銜接維度。學生能否聯系起“組成三角形”和“兩點之間線段最短”兩個知識點。第二，知識維度。學生是否了解判斷“三條線段能否組成三角形”的一般方法，學生是否知道“三邊關系”的理論依據就是“兩點之間線段最短”。第三，能力維度。學生能否從三角形三邊的一般關系，發現最簡便方法，總結出“最短兩邊之和大于第三邊”規律。

（一）改轍易途，對接經驗真實自然

制訂教學目標時，教師應針對學生的知識基礎，結合具體學情，從活動設計方面進行改變，改轍易途，讓課堂自然而真實。

片段之一：

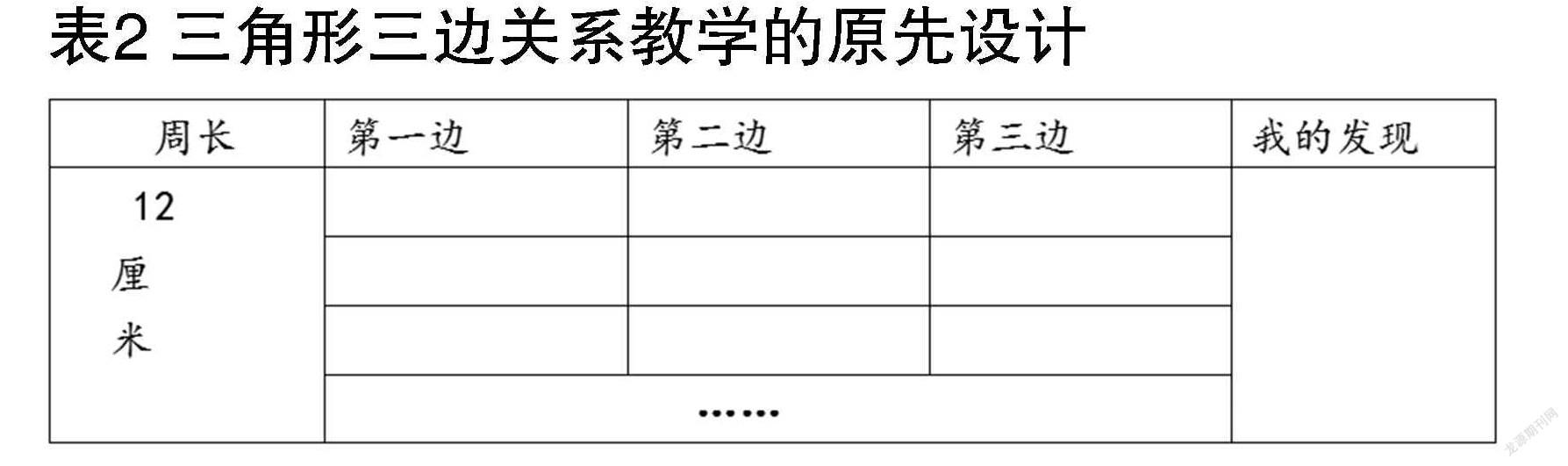
筆者原先是這樣安排教學的：出示周長是12厘米形狀不同的三角形，并分別量出三條邊的長度，如表2所示。

之后，筆者改善了原教學中由三條小棒拼三角形的設計，轉而提供周長都是12厘米的三角形，讓學生認識到周長一樣的三角形，由于三邊長度不同，形狀也是不同的，改善了原教學只重視可以圍成三角形的三邊的研究。

（二）固本正源，借力猜想任務驅動

有意義的數學學習需要把目標變為任務，把知識變成問題，把方法變為問題。學生需要經歷體驗的過程，才能發現和理解三角形三邊關系。在以往教學中，教師只是讓學生量一量三角形三邊的長度，這樣的體驗空間太小。于是，筆者設計了第二次教學方案。

片段之二：

教師問：“用12厘米的細鐵絲圍成一個三角形，你覺得三條邊的長度可能是多少？（每邊長度取整厘米數）”

學生1回答： “4、4、4。”

學生2回答：“3、4、5。”

學生3回答： “1、4、7。”

學生4回答：“ 5、5、2。”

教師可以讓學生猜一猜三角形的三邊可能會是什么情況，由于是同一根鐵絲圍成的三角形，總長是相等的，學生理所當然以為無論怎么分，都可以圍成三角形。事實上，由于分成不同的長度，有的長度是不可以圍成三角形的。教師借助這樣的設計，激發了學生深入研究的興趣。

二、基于核心目標的深度扣問，延伸體驗，課堂深入厚實

思考是數學教育的本真，教師要讓學生在動態過程中尋找三角形三邊本質關系，在沖突中思考，在探究中反思，凸顯數學思考的價值取向。

（一）提領而頓，聚焦核心高峰體驗

教師要確定課堂核心目標，深挖隱藏在背后的數學思想，幫助學生體驗和感悟數學知識。

片段之三：

教師問：“手里的細鐵絲按照剛才反饋的每組三條邊的長度，折一折、圍一圍，你發現什么？”

學生1回答：“三條邊的總長度相同。”

學生2回答：“有些可以圍成三角形，有些不能圍成三角形。”

學生3回答：“當兩邊之和小于第三條邊時圍不成一個三角形。（課件展示不能圍成三角形的三條邊）”

學生4回答：“3+4>5，所以能圍成一個三角形。”

在學生反饋以后，教師組織討論：“同樣長的鐵絲折成三段，為什么有的三條邊可以圍成三角形，有的不能？”

數學需要理性的思考，教師要在課堂上充分調動學生思考，通過操作讓學生明白內涵，并經過分析充分地表達出來。

（二）本立道生，實現從本到意的突圍

教師的課堂教學不應該只滿足于知識的傳輸，更要幫助學生關注知識結構，構建數學思維，把數學思想與方法當作學習的根本，讓數學學習彰顯數學思想的力量。

片段之四：

教師問：“那7+3>2是不是也可以圍成一個三角形？ ”

學生1回答：“好像不行！ ”

學生2回答：“我發現有的三條線段有2組線段之和大于第三條邊的。 ”

學生3回答：“我知道，不能只看其中兩條邊相加的和大于第三邊，必須每兩邊相加與第三邊比大小，才可以圍成一個三角形。 ”

教師問：“能不能重新概括一下，并完整地說一說其中的規律？ ”

學生4回答：“應該是任意兩邊之和大于第三邊，這樣的三條邊能組成三角形。 ”

教師問：“三角形任意兩邊之和大于第三邊，還有其他理由來解釋嗎？ ”

學生5回答：“像上面的三角形中，我們可以把線段AB 看作是A和B之間的距離，A點經過C到B也可以看作A和B之間的距離，我們已經知道了兩點之間線段最短，所以BC+AC>AB。 ”

學生6回答：“這樣還是不完整的，我們可以把線段AC 看作是A和C之間的距離，A點經過B到C也可以看作A和C之間的距離，我們已經知道了兩點之間線段最短，所以AB+BC>AC;同樣的AB+AC>BC。 ”

學生7回答：“老師，兩點之間的線段長度要比兩點之間的折線要短，兩點之間線段最短。 ”

教師問：“判斷能不能圍成一個三角形，看來大家都掌握了，你們能不能改進一下，使得更為方便呢？ ”

學生8回答： “只要最短的兩條邊的和大于第三邊就可以了。 ”

由于同樣長的鐵絲可以分成不同的長度，出現不同的結果，學生會發現能圍成三角形的有兩邊之和大于第三邊，不能圍成三角形的也有兩邊之和大于第三邊，發現“最短的兩邊之和大于第三邊”的規律。這樣，學生不僅收獲了數學知識，還充分運用了數學思想，實現了課堂教學從本到意的突圍。

（三）追本求源，由表及里順勢而為

數學課堂是一個動態的過程，蘊含著數學本質的關鍵點，教師應該引導學生尋找思維源頭，由表及里，實現有意義的數學學習。

片段之五：

教師問：“把一根長15厘米的鐵絲折成一個三角形，最長的一段鐵絲應該是多少，你是怎么想的？ ”

學生1回答：“15除以3是5，比5多1就是6厘米。 ”

學生2回答：“不對，那我比6厘米多一點，7厘米也可以吧。 ”

學生3回答：“那8不可以嗎？ ”

學生4回答：“如果是8厘米的，剩下還有7厘米，那這個三角形算3、4、8厘米，根據剛才學的兩條短邊之和大于最長邊，3+4<8。 ”

教師問：“學生非常會思考，那么最長這條邊應該滿足怎樣的要求呢？ ”

學生5回答：“我覺得把15厘米先分成兩段，分別是8厘米和7厘米，7厘米作為最長邊， 再把8厘米分成兩條短邊就可以了。 ”

教師問：“這位學生講得非常有道理，想想可以是哪些三角形？ ”

學生7回答：“如1、7、7，或2、6、7，或3、5、7。 ”

教師讓學生討論“一根鐵絲折成一個三角形，最長一段是多少”，可以啟發學生總結出“兩條短邊之和大于第三邊”的規律，并感悟到最長的邊雖然要比另外兩條邊長，但不能大于它們的和。教師不斷啟迪學生的思維，讓課堂有了別樣的精彩。

三、基于學習差異的現實存在，求同存異

學生都是不同的生命體，有著各自不同的思考方式，教師不能用相同教學目標評價學生，應該直面學生存在的差異。

片段之六：

教師用兩根長度分別是4厘米和5厘米的小棒圍成一個三角形，問學生：“第三條邊最短可能是多少，最長可能是多少？”

剛剛還沉浸在發現“兩條短邊之和大于第三邊就能組成一個三角形”這個規律之中的學生，又重新進入新的思維狀態。

學生1回答：“把5作為長邊，想4+（ ）>5 ，4+2>5所以最短的為2。 ”

學生2回答：“把5作為長邊，那么5-4=1，這樣短的兩邊剛好與長邊一樣，這樣不能拼成一個三角形，所以1再增加1厘米就可以拼成一個三角形，于是5-4+1=2厘米。 ”

學生3回答：“把未知這條邊看作最長邊，那么? 4+5>（? ?），最長可以是8。 ”

學生4回答：“把未知這條邊看作最長邊，那么已知的4和5作為短邊，根據兩條短邊之和大于第三邊，所以4+5=9，再減少1厘米就可以成為三角形 4+5-1=8厘米。 ”

設置這樣的問題具有挑戰性，由于學生的認知方式不同，會存在客觀的個體差異。教師要接受這種差異，不用整齊劃一的標準衡量學生，給予不同學生不同的評價標準。

參考文獻：

[1]曾嫻秋.指向數學深度學習的進階性大問題設計研究——《三角形的三邊關系》教學設計研究[J].新智慧，2021（4）.

（作者單位：浙江省臺州市天臺縣赤城街道第二小學）