理解數學本質凸顯以生為本

陳家才 段志貴

摘 要：在某高中視導過程中通過課堂觀察發現，教師的傳統教學理念根深蒂固，課堂教學中教師急著替學生畫圖、思考、解題，仍然是教師一講到底，缺乏以生為本的理念，課堂教學中教師仍然是就題論題，沒有結合數學固有特性對課堂內容進行深度加工.結合目前課堂教學中現象，教師如何把握數學本質設計以生為本的課堂是值得研究的問題.

關鍵詞：傳統教學理念；數學本質；以學為主

1 視導中發現的問題

在某高中視導過程中通過課堂觀察發現，教師的傳統教學理念根深蒂固，課堂教學中教師急著替學生畫圖、思考、解題，仍然是教師一講到底，缺乏以生為本的理念，課堂教學中教師仍然是就題論題，沒有結合數學固有特性對課堂內容進行深度加工.已有研究認為數學本質是蘊含在“數學知識形成”和“數學問題解決”過程中的數學思想和數學精神［1］.結合目前課堂教學中現象，教師如何把握數學本質設計以生為本的課堂呢？本文以蘇教版“5.1函數的概念”的教學設計為例探尋以生為本的教學策略.

2 指向以生為本的函數概念教學流程設計

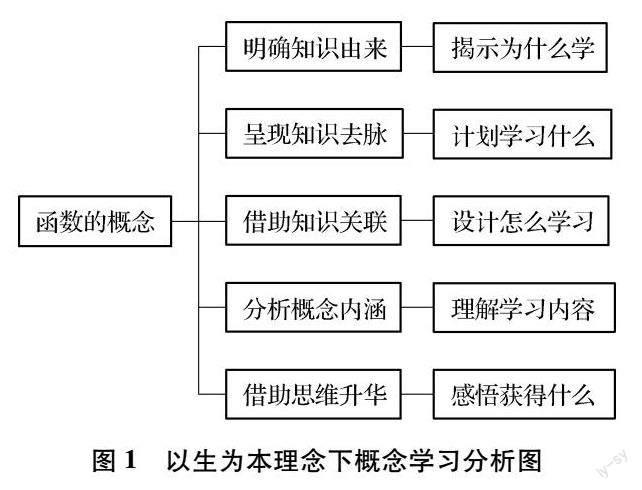
以生為本的教學設計離不開教師對數學知識本質的理解，這是組織和實施課堂教學的出發點，也是歸宿點.為此，教師要知道知識的來龍去脈，要厘清知識的內在關聯，要深度分析概念的基本內涵，要理解問題解決過程中的數學思想.我們研究指向以生為本的教學設計必須明確“為什么學”“學習什么”“怎么學習”“理解學習內容”“感悟獲得什么”等基本問題，充分把握課堂教學設計的主線，具體流程如下（圖1）.

2.1 明確知識由來，揭示為什么學

從1673年萊布尼茨的手稿創造了“函數”一詞，到1939年布爾巴基學派給出函數的定義，縱看函數定義的演變過程，“單值對應”是函數概念的最本質特征.創設這樣一個真實情景：

問題1：三峽大壩最大蓄水393億立方米.校核洪水位以下的水庫容積稱為總庫容，即水位達到185.40米時的蓄水量.水庫工作人員是借助水庫里的標示水位的桿子知道水位，為什么知道水位就能確定蓄水量？這里的蓄水量與水位有怎樣的關系呢？

依據學生的認知過程創設三峽大壩蓄水量與水位關系的教學情景，不僅落實了立德樹人的根本任務，提升學科素養，凸顯以生為本，讓教師扮演助學、導學角色，還能使學生化身已有認知基礎上，把握知識的本質.一言以敬之，這種問題的切入方式能啟發學生思考，讓學生感覺過渡自然，有利于學生感悟知識與實際生活之間關聯.

2.2 呈現知識去脈，計劃學習什么

前面已經學習了函數的概念，為什么現在還要學習函數，這是本節課教學重點，在上面問題1之后，學生從初中函數出發，回憶“變量說”，復習函數的三種表示方法，為后面提出3個實例起到前后呼應作用，奠定了學習新知的基礎.

問題2：在初中學習了“函數”，請舉出你熟悉的函數例子.

追問1：這位同學所舉的函數例子是怎樣表示的？

追問2：請你給出初中函數的概念.

追問3：請你分析以下3個問題.

這個追問3是關鍵，直擊高中為什么還要再學習函數的問題，初中函數是刻畫兩個變量的變化過程，沒有提到符號f（x）、定義域、值域，沒有提及對應關系.可以預設學生對追問3的3個問題的回答存在爭議，有的同學說y不是x的函數，有的同學說y是x的函數，學生又無法說明是與不是的理由，引出再次學習函數的概念的必要性.

2.3 借助知識關聯，設計怎么學習

本節的難點是如何借助3個實例，讓學生經歷觀察、比較、分析，探究3個實例共性，高度概括出一般規律，把握“對應關系”的本質，讓學生形成一般性思考問題的習慣，使學生的素養達到數學抽象水平.初中學習過的函數概念是“變量說”，沒有明確定義域、值域、對應關系，高中函數的表達呈現是“集合說”，為了重點突出自變量的范圍對函數影響，更加符合學生的認知，對教材中問題的順序進行了調整，將第2個問題變成第1個情景，第1個問題變成第2個情景，通過5個遞進式問題，讓問題的解決過程能夠可視化.

情景1：一物體從靜止開始下落，下落的距離y（單位：m）與下落時間x（單位：s）之間近似地滿足關系式y=4.9x2.若一物體下落2s，你能求出它下落的距離嗎？

追問1：若物體下落2s，你能求出它下落的距離嗎？若物體下落4s，2s？

追問2：下落的距離y是下落時間x的函數？為什么？

追問3：物體靜止時離地面距離為19.6m，經過3s，你能求出它下落的距離嗎？

追問4：在追問3的情景下，y與x的對應關系如何表達才能更準確呢？

追問5：請你完成表1.

追問1—2引導學生通過解決問題溫習了初中的函數定義，追問3—5指向函數自變量的取值范圍，讓學生在追問3情景中思考、表達、反思對應關系，函數自變量的取值范圍不一樣，則不是同一個函數.通過具體的情景具體的問題追問3—5，讓數學抽象的過程變得簡單易懂.追問1—5讓學生經歷“實例—觀察、比較、分析—抽象”的過程，概括出函數自變量的取值范圍是函數必不可少的一部分，培養學生數學抽象、邏輯推理等能力.情景1的探究過程喚醒了學生抽象思維，再研究情景2人口數量變化趨勢、情景3某市一天24小時內的氣溫變化圖對函數概念的影響，學生已經具備了基本的抽象和分析能力.

從情景1我們研究了函數的自變量范圍對函數的影響，理解了函數自變量范圍不同，兩個函數不是同一個函數.初中時學生學習過自變量、函數值、函數關系，接下來我們會研究什么對函數的影響呢？學生類比剛學過研究函數自變量范圍的方法，進而研究函數值范圍、函數關系對函數的影響，從而理解函數的本質.

情景2：人口數量變化趨勢是我們制定一系列相關政策的依據.從中國統計年鑒中可以查得我國1979—2014年人口數據資料（年末）如表2所示，你能根據該表說出我國人口的變化情況嗎？

追問1：1979年我國人口數是多少呢？1999年呢？

追問2：人口數是年份的函數嗎？能寫出函數的表達式嗎？

追問3：請你寫出人口數的集合B.

追問4：若將集合B改為集合{y1979≤y≤2014}，兩個函數是否為同一個函數，為什么？

追問5：基于追問4的分析，你能舉出表示同一個函數的例子嗎？為什么？

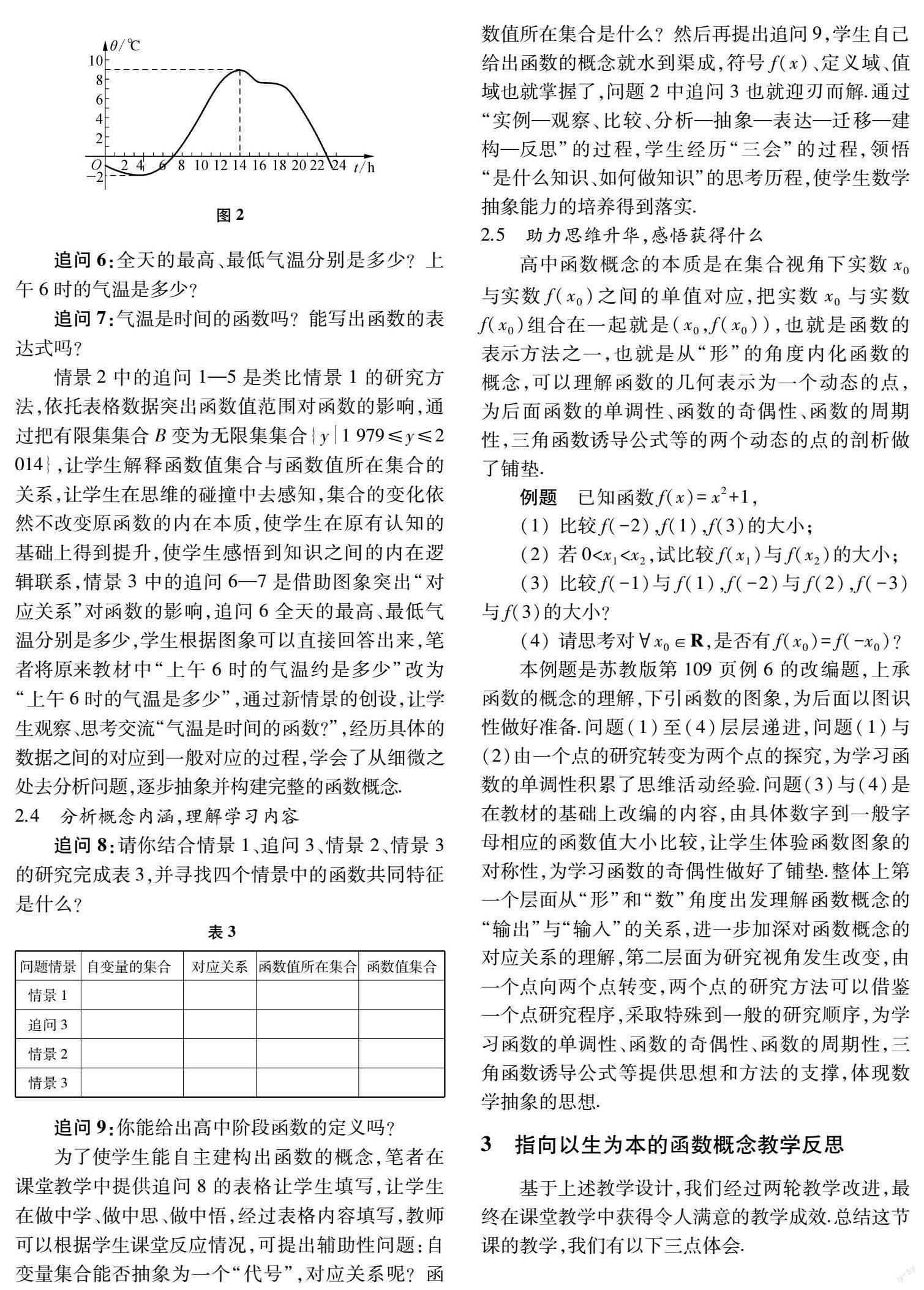
情景3：圖2為某市一天24小時內的氣溫變化圖.

追問6：全天的最高、最低氣溫分別是多少？上午6時的氣溫是多少？

追問7：氣溫是時間的函數嗎？能寫出函數的表達式嗎？

情景2中的追問1—5是類比情景1的研究方法，依托表格數據突出函數值范圍對函數的影響，通過把有限集集合B變為無限集集合{y1979≤y≤2014}，讓學生解釋函數值集合與函數值所在集合的關系，讓學生在思維的碰撞中去感知，集合的變化依然不改變原函數的內在本質，使學生在原有認知的基礎上得到提升，使學生感悟到知識之間的內在邏輯聯系，情景3中的追問6—7是借助圖象突出“對應關系”對函數的影響，追問6全天的最高、最低氣溫分別是多少，學生根據圖象可以直接回答出來，筆者將原來教材中“上午6時的氣溫約是多少”改為“上午6時的氣溫是多少”，通過新情景的創設，讓學生觀察、思考交流“氣溫是時間的函數？”，經歷具體的數據之間的對應到一般對應的過程，學會了從細微之處去分析問題，逐步抽象并構建完整的函數概念.

2.4 分析概念內涵，理解學習內容

追問8：請你結合情景1、追問3、情景2、情景3的研究完成表3，并尋找四個情景中的函數共同特征是什么？

追問9：你能給出高中階段函數的定義嗎？

為了使學生能自主建構出函數的概念，筆者在課堂教學中提供追問8的表格讓學生填寫，讓學生在做中學、做中思、做中悟，經過表格內容填寫，教師可以根據學生課堂反應情況，可提出輔助性問題：自變量集合能否抽象為一個“代號”，對應關系呢？函數值所在集合是什么？然后再提出追問9，學生自己給出函數的概念就水到渠成，符號f（x）、定義域、值域也就掌握了，問題2中追問3也就迎刃而解.通過“實例—觀察、比較、分析—抽象—表達—遷移—建構—反思”的過程，學生經歷“三會”的過程，領悟“是什么知識、如何做知識”的思考歷程，使學生數學抽象能力的培養得到落實.

2.5 助力思維升華，感悟獲得什么

高中函數概念的本質是在集合視角下實數x0與實數f（x0）之間的單值對應，把實數x0與實數f（x0）組合在一起就是（x0，f（x0）），也就是函數的表示方法之一，也就是從“形”的角度內化函數的概念，可以理解函數的幾何表示為一個動態的點，為后面函數的單調性、函數的奇偶性、函數的周期性，三角函數誘導公式等的兩個動態的點的剖析做了鋪墊.

例題 已知函數f（x）=x2+1，

（1） 比較f（-2），f（1），f（3）的大小；

（2） 若0＜x1＜x2，試比較f（x1）與f（x2）的大小；

（3） 比較f（-1）與f（1），f（-2）與f（2），f（-3）與f（3）的大小？

（4） 請思考對x0∈R，是否有f（x0）=f（-x0）？

本例題是蘇教版第109頁例6的改編題，上承函數的概念的理解，下引函數的圖象，為后面以圖識性做好準備.問題（1）至（4）層層遞進，問題（1）與（2）由一個點的研究轉變為兩個點的探究，為學習函數的單調性積累了思維活動經驗.問題（3）與（4）是在教材的基礎上改編的內容，由具體數字到一般字母相應的函數值大小比較，讓學生體驗函數圖象的對稱性，為學習函數的奇偶性做好了鋪墊.整體上第一個層面從“形”和“數”角度出發理解函數概念的“輸出”與“輸入”的關系，進一步加深對函數概念的對應關系的理解，第二層面為研究視角發生改變，由一個點向兩個點轉變，兩個點的研究方法可以借鑒一個點研究程序，采取特殊到一般的研究順序，為學習函數的單調性、函數的奇偶性、函數的周期性，三角函數誘導公式等提供思想和方法的支撐，體現數學抽象的思想.

3 指向以生為本的函數概念教學反思

基于上述教學設計，我們經過兩輪教學改進，最終在課堂教學中獲得令人滿意的教學成效.總結這節課的教學，我們有以下三點體會.

3.1 教學設計要瞄準數學思想，加強學生理解數學本質

以生為本的教學設計要整體規劃，培養學生的創造性思維.教師不僅要把握冊與冊知識點之間的關系、課時與課時之間的關系、概念之間的關系，還要從整體上把握知識的定位.函數的本質是單值對應，把實數x0與實數f（x0）結合在一起也就是研究（x0，f（x0）），此時研究的是一個點的問題，而函數的單調性、函數的奇偶性、函數的周期性、三角函數誘導公式等是以兩個點研究為切入點的，因而可以借“一點”研究的力，繼續研究“兩點”的問題.

3.2 教學過程設計要立足學情特點，優化課堂教學情景

以生為本的教學設計要把握數學知識本質，站在學生視角思考問題，將學生轉變為學習的主人，激發學生的求知欲.本節課的內容與舊教材比較增加了初中函數定義的陳述，增加了蘊含變量說和對應說之間本質區別的3個核心問題，部分教師在教學時忽略初高中函數的銜接.在原先設計中筆者按照課本情景順序處理，學生面對不熟悉情景顯得被動接受，在課堂上學生沒有進行深度思考.為讓學生能輕松進入情景集中思考，筆者對情景呈現的順序進行了調整.初中的函數教學基于具體背景，教材中的情景2物體的下落適合學生的思維起點，從學生的認知經驗出發，將教材中的情景2調整為情景1設置追問，有利于學生深入情景，探究新知.情景1的追問是對函數概念的再次拷問，以此引出再次研究函數概念的必要性，從而提高學生的邏輯推理、數學抽象的能力.

3.3 教學手段設計要選擇合適載體，引領學生深度領悟

以生為本的教學設計要以核心素養作為教學目標追求，借助三會，達成學科核心素養.數學抽象是從具體到一般的探究過程，尋找諸多情景的共性并用數學語言加以精準的刻畫.如何讓“核心素養”看得見、講得清，這是教師面臨的一個困境.本節課通過表格填寫—觀察表格—共性分析—抽象概括的過程實現素養達成.具體在本文中出現了2次，情景1的出現順應了學生的思維起點，情景1與追問3自變量的集合不一樣，函數的表達式一樣，產生思維上的沖擊，引發學生深度思考.

另外一次是在情景3中出現的，學生通過完成表格，發現情景1、情景1的追問3、情景2、情景3的自變量的集合不一樣，情景1、情景2、情景3的對應關系是不一樣的，函數值集合是不一樣的，繼而教師提出輔助性問題“自變量集合能否抽象為一個‘代號，對應關系呢？函數值所在集合呢”，借助表格填寫使學生處于核心概念的最近發展區，使“數學抽象”摸得著看得見.在這樣的情景中學生領悟到數學抽象的操作步驟，再次體驗特殊到一般思想.

以生為本的課堂要瞄準素養目標，創設符合學生認知過程的情景，引導學生理解數學本質，立足知識體系整體規劃，一以貫之.力求在每節課中落實以生為本的教學理念，教師還需要在教學目標、教材分析、學情分析、活動設計等方面不斷反思、提煉、實踐.

參考文獻：

［1］ 徐德同，黃金松.關于“理解數學把握本質”的幾點思考［J］.數學通報，2022，61（3）：3740.

［2］ 史寧中.數形結合與數學模型［M］.北京：高等教育出版社，2018.