經歷探究過程 理解數學本質

張秀頎

[摘 要]讓學生經歷探究過程能促進學生深入理解數學本質，從而讓數學學習更高效。在“角的度量”一課中，先在導入環節引發學生認知上的沖突，從而引入概念，然后引導學生動手操作，讓學生經歷探究的過程，進而理解數學本質和習得數學技能。

[關鍵詞]數學本質；探究過程；角的度量

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2017）29-0036-01

數學課程標準特別強調“在數學教學中引導學生經歷數學探究的過程，從而使數學知識和數學技能在學生腦海里扎根”。那么，在“學為中心”的小學數學課堂上，應如何引導學生經歷探究的過程，從而讓他們理解數學的本質呢？下面我結合“角的度量”的教學談談幾點做法。

一、引發認知沖突，引入角度概念

在“角的度量”一課的導入環節，我給學生出示了圖1，然后讓學生討論：“哪個滑梯下滑的速度更快？”有些學生覺得1號滑梯能滑動得更遠；有學生覺得2號滑梯更加平緩，也有學生認為3號滑梯特別陡峭、驚險……學生對此產生了認知沖突：滑梯坡度到底是什么？經過對比，學生發現三個滑梯長短不一、坡度不一、大小不一，進而達成共識：滑梯坡度是影響滑動速度的主要因素。我將坡度在圖中標記出來，然后將圖形簡化為三個角，引導學生觀察這三個角，并比較角的大小（圖2）。

學生就“∠1比∠2大多少”這個問題展開了討論，通過討論發現：只有運用量角器進行準確度量，才能知道角的大小。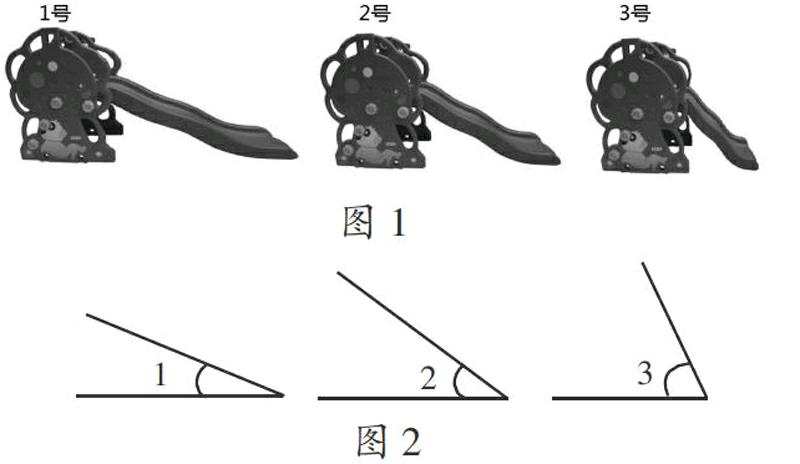

這樣，借助認知沖突引入角度概念，激發了學生的探究熱情，為后續的深度研究埋下了基石。

二、借助動手操作，感知角度度量工具，內化角度概念

量角器是數學教材里的一個抽象概念，如果不讓學生經歷量角器的發展演變歷程，他們就不能深入了解量角器，自然不能在實際操作中用好量角器。因此，我要求學生 “自制”量角器，讓他們經歷量角器的形成過程。

首先，我讓學生在沒有量角器的條件下，想辦法動手測量出一個角的度數。經過思考，學生想出了借助三角尺度量的方法，并通過小組合作制作了“標準角”（如圖3所示），用于測量角度的大小。

其次，我引導學生思考“為什么用‘標準角量出來的度數不盡相同？”，從而使學生發現“標準角疊得不一樣，所以測量結果也不盡相同”，從而明白要度量角應統一好“標準角”。

最后，在我的提示與引導下，學生以半圓形紙片為工具，動手自制了“量角器”（見圖4）。我要求學生對比觀察教材中提供的量角器圖形，找出自制量角器和教材量角器的共同點。通過對比，學生找出了自制量角器和教材量角器的共同點：都是半圓形，內外圈標記有刻度。

在以上教學環節中，我分步引導學生動手制作簡單的量角器，讓學生經歷了量角器的形成過程，促進了學生對量角器及角度概念的深層次理解。

img src="http://img1.qikan.com.cn/qkimages/xisx/xisx201710/xisx20171018-2-l.jpg" alt="" />

三、動手操作實踐，習得“量角”技能

測量角度是本節課教學的重點，也是難點。對此，我先讓學生自主測量，然后小組演示和交流。通過交流和討論，學生確定了量角器測量角度的主要步驟：先將量角器的中心和角的頂點對齊，之后再將量角器的零刻度線與角的一條邊重合。這時，有學生提出疑問：“刻度上有兩圈刻度，要讀哪一個呢？”我讓學生帶著問題自己去嘗試測量。通過測量，學生發現了讀數的規律：如果開始的邊在0的內圈，就按照內圈來讀數，如果是在0的外圈就讀外圈的數。根據學生發現的規律，我讓學生進行測量鞏固訓練，幫助學生掌握“兩重一看”的測量方法。

綜上可知，教師引導學生經歷數學操作探究的過程，能使學生一步步走進知識的內核，經歷知識的形成過程，從而觸及知識的本質，真正掌握知識。

（責編 黃春香）endprint